Reproduce the Results

Recently, I found an open access review article¹ about simulation in soft robots. What makes it especially valuable is that the authors have also shared the original .mph and .wbpz files in supporting information.

Solid Mechanics

The authors did not use Component - Materials to define the materials of the soft gripper. Instead, they directly define the materials in Solid Mechanics - Hyperelastic Material.

Part of the following content of this section is from Finite Element Modeling of Soft Fluidic Actuators: Overview and Recent Developments.

Fundamentals of Continuum Mechanics

The deformation of a solid can be described by the relationship between the spatial coordinate frame x (current configuration) and the material coordinate frame X (original configuration) as

$$\mathbf{x}=\mathbf{x}(\mathbf{X}, t)=\mathbf{X}+\mathbf{u}$$

where u is the displacement vector.

The deformation gradient is given by

$$\mathbf{F}=\frac{\partial \mathbf{x}}{\partial \mathbf{X}}=\mathbf{I}+\frac{\partial \mathbf{u}}{\partial \mathbf{X}}=\left[\begin{array}{lll} \frac{\partial x}{\partial X} & \frac{\partial x}{\partial Y} & \frac{\partial x}{\partial Z} \\ \frac{\partial y}{\partial X} & \frac{\partial y}{\partial Y} & \frac{\partial y}{\partial Z} \\ \frac{\partial z}{\partial X} & \frac{\partial z}{\partial Y} & \frac{\partial z}{\partial Z} \end{array}\right]$$

F is the Jacobian matrix of the transformation from X to x; hence, $J=\operatorname{det}(\mathbf{F})$ is the local volume scale factor. For an incompressible material, $J=1$.

The polar decomposition theorem states that any second-order tensor can be decomposed into a product of pure rotation (R) and a symmetric deformation tensor (U the right stretch tensor or V the left stretch tensor)

$$\mathbf{F}=\mathbf{R} \mathbf{U}=\mathbf{V} \mathbf{R}, \quad \mathbf{R}^T \mathbf{R}=\mathbf{R} \mathbf{R}^T=\mathbf{I}$$

Thus

$$\mathbf{F}^T \mathbf{F}=(\mathbf{R} \mathbf{U})^T \mathbf{R} \mathbf{U}=\mathbf{U}^T \mathbf{U}=\mathbf{U}^2=\mathbf{C}$$ $$\mathbf{F} \mathbf{F}^T=\mathbf{V R}(\mathbf{V R})^T=\mathbf{V} \mathbf{V}^T=\mathbf{V}^2=\mathbf{B}$$

where C is the right Cauchy–Green deformation tensor, and B is the left Cauchy–Green deformation tensor. C and B admit the same three principal invariants $I_1$, $I_2$, and $I_3$ given by

$$I_1=\operatorname{tr}(\mathbf{C}), \quad I_2=\frac{1}{2}\left(\operatorname{tr}(\mathbf{C})^2-\operatorname{tr}\left(\mathbf{C}^2\right)\right), \quad I_3=\operatorname{det}(\mathbf{C})$$

From the polar decomposition, $\mathbf{F}=\mathbf{R U}=\mathbf{V R}$, it follows immediately that

$$\mathbf{U}=\mathbf{R}^{\mathrm{T}} \mathbf{V} \mathbf{R} .$$

While geometrically speaking, it makes no difference whether we view the motion as being a rotation followed by a pure stretch or as a pure stretch followed by a rotation, they do lead to two different stretch tensors ( $\mathbf{U}$ or $\mathbf{V}$) whose components have different geometrical meanings. Furthermore, based on these two stretch tensors, two commonly used deformation tensors are defined, the so-called right Cauchy-Green tensor $\mathbf{C}\left(\equiv \mathbf{U}^2\right)$ and the left Cauchy-Green tensor $\mathbf{B}\left(\equiv \mathbf{V}^2\right)$. In Chapter 5, we show that the tensor $\mathbf{B}$ is objective (independent of observer), whereas the tensor $\mathbf{C}$ is nonobjective. This important difference is relevant to the formulation of the constitutive equations for a continuum under large deformation.²

According to Rivlin’s phenomenological theory, rubber is assumed isotropic in elastic behavior and very nearly incompressible. The elastic properties of a rubber can be explained in terms of a strain energy function based on the strain invariants I1, I2 and I3. This theory offers a mathematical framework to describe rubbery behavior based on continuum mechanics. In this approach, stress and strain analysis problems may be solved independent of the microscopic system or molecular concepts and the elasticity theory can be the starting point of any kind of modeling effort as follows (Boyce and Arruda, 2000; Achenbach and Duarte, 2003; Pucci and Saccomandi, 2002; Yeoh and Fleming, 1997; Chang et al., 1991):

$$W = f(I_1, I_2, I_3) =\sum_{i+j+k=1}^{\infty} C_{i j k}\left(I_1-3\right)^{i} \cdot\left(I_2-3\right)^{j} \cdot\left(I_3-1\right)^{k}$$

where $W$ (sometimes written as $U$) is the strain energy density or stored energy function defined per unit volume. $I_1$, $I_2$ and $I_3$ are given in principle extension ratios $\lambda_1$, $\lambda_2$ and $\lambda_3$ by:³

$$\begin{aligned} & \mathrm{I}_1=\lambda_1^2+\lambda_2^2+\lambda_3^2 \\ & \mathrm{I}_2=\lambda_1^2 \lambda_2^2+\lambda_2^2 \lambda_3^2+\lambda_3^2 \lambda_1^2 \\ & \mathrm{I}_3=\lambda_1^2 \lambda_2^2 \lambda_3^2 \end{aligned}$$

Hyperelastic Material Models

The deformation of soft actuators, especially under pressure, is highly nonlinear. That means simple linear models (like those used for rigid materials) don’t work well for soft materials, which can stretch far beyond their original shape. To accurately model these deformations, hyperelastic material models are used, which take into account the large strains (deformations) that soft materials experience.

These models, such as Neo-Hookean, Mooney–Rivlin, Ogden, and Yeoh, describe the relationship between stress and strain in materials that undergo large deformations. For soft actuators, these models allow us to simulate how the material behaves under pressure and how it returns to its original shape once the pressure is released.

Polynomial Model (Generalized Rivlin Model)

$$W=\sum_{i=0, j=0}^n C_{i j}\left(I_1-3\right)^i\left(I_2-3\right)^j$$

This model is often truncated in terms of the second and third order.

Mooney–Rivlin Model

$$W=C_1\left(I_1-3\right)+C_2\left(I_2-3\right)$$

This model is used for moderate deformation, i.e., lower than 200%.

Ogden Model

$$W=\sum_{n=1}^N \frac{\mu_n}{\alpha_n}\left(\lambda_1^{\alpha_n}+\lambda_2^{\alpha_n}+\lambda_3^{\alpha_n}-3\right)$$

Six parameter model (N = 3) is the most used for large strain problems, i.e., at or above 400%.

Experimental results show that $\frac{\partial W}{\partial I_1}$ is approximately constant, and that $\frac{\partial W}{\partial I_2}$ decreases with the amount of strain. Therefore, one simplification is to ignore terms in $I_2$.

Yeoh Model

$$W=C_1\left(I_1-3\right)+C_2\left(I_1-3\right)^2+C_3\left(I_1-3\right)^3$$

Also, one of the most used models for large strain problems, i.e., at or above 400%.

Neo-Hookean Model

This model is offered only in terms of the first deviatoric invariant (Timbrell et al., 2003). By setting $N = 1$, $\alpha_1 = 2$ in the Ogden model, the neo-Hookean can be offered (Bol and Reese, 2003):

$$W=C_1\left(I_1-3\right)=\frac{\mu}{2}\left(I_1-3\right)$$

where $\mu$ is the shear modulus. Good agreement for small strains, i.e., lower than 50%.

Parameters

As stated above, the authors directly define materials in Solid Mechanics - Hyperelastic Material. Many studies have already measured various parameters of materials like Ecoflex™ 00-30.

Table: Material Parameters for Ecoflex as an Incompressible Material⁴

Ogden ($N=3$)	Gent	Yeoh	Mooney-Rivlin
$\mu_1=22\text{kPa}$	$J_m=27$	$C_1=17\text{kPa}$	$C_1=48\text{kPa}$
$\alpha_1=1.3$	$\mu_=17\text{kPa}$	$C_2=-0.2\text{kPa}$	$C_2=-152\text{kPa}$
$\mu_2=0.4\text{kPa}$		$C_3=0.023\text{kPa}$
$\alpha_2=5$
$\mu_3=-2\text{kPa}$
$\alpha_3=-2$

Contact

A contact pair consists of a source boundary and a destination boundary. When the model deforms, these two surfaces may come into contact with each other. To prevent them from penetrating or overlapping, a Contact Pair must be defined.

Geometry

The following model was exported from COMSOL file provided by the authors.

Boundary loads are applied to the continuous internal cavities:

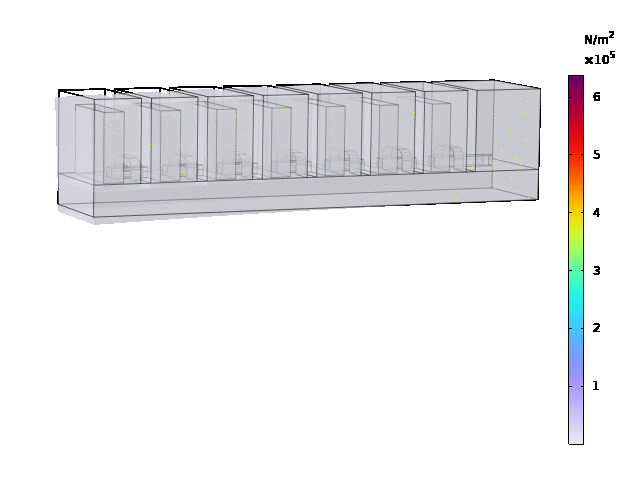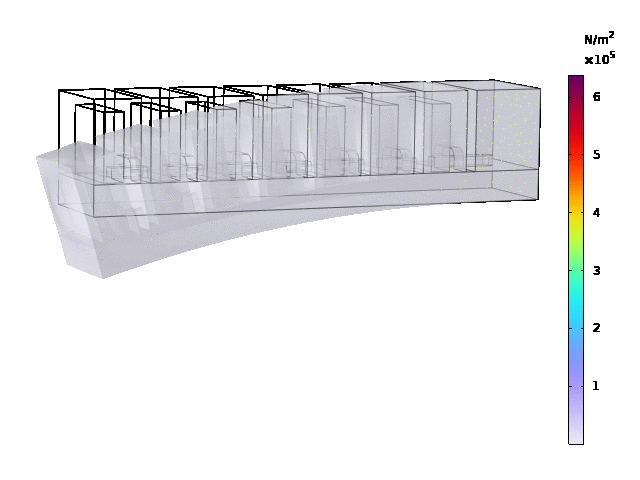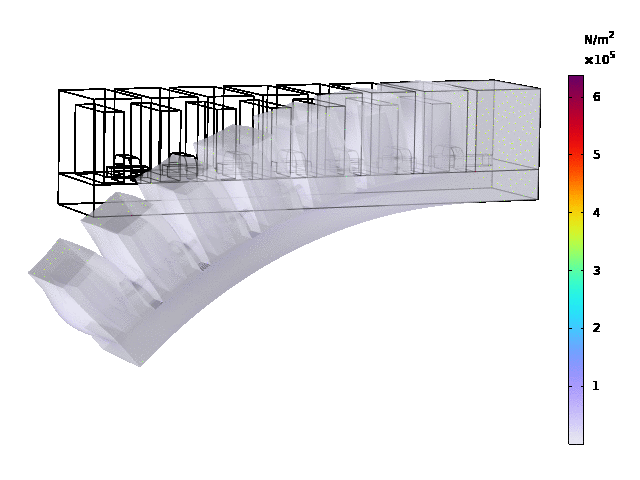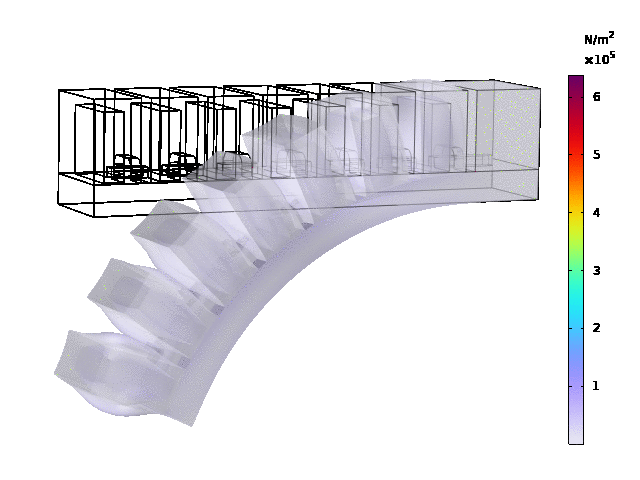
Results

The load type is pressure $p = \mathrm{pressure} \times \mathrm{ramp}$ , and ramp was set to range(0.02,0.02,0.3), pressure was set as 25[kPa].

Stationary study:

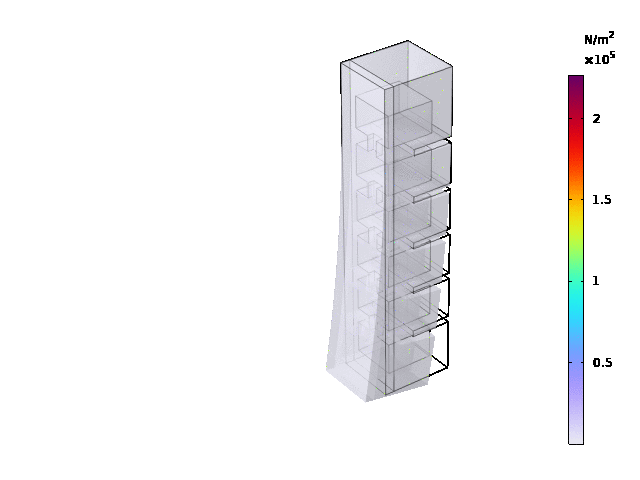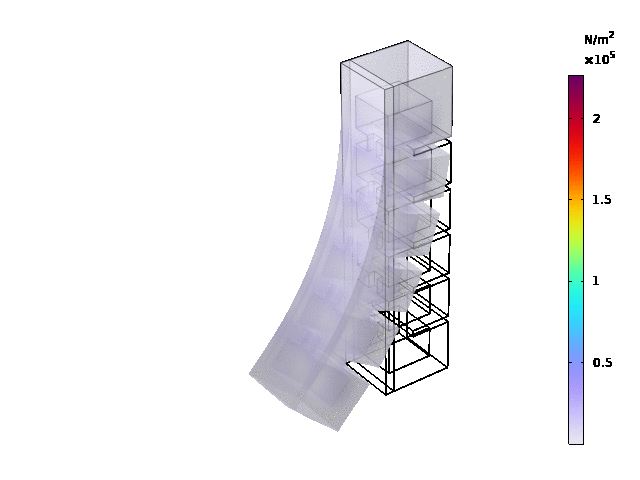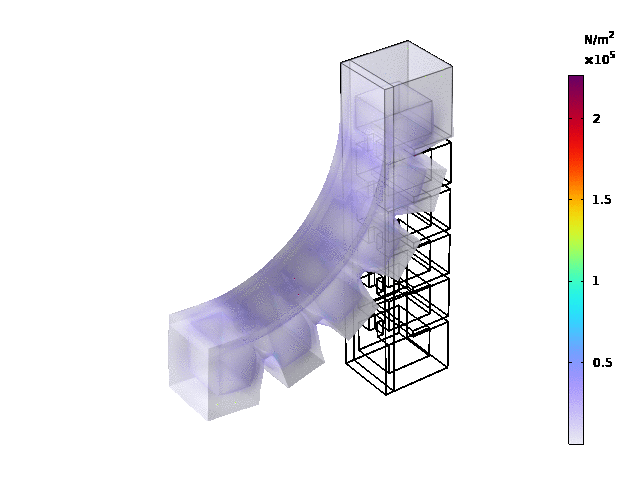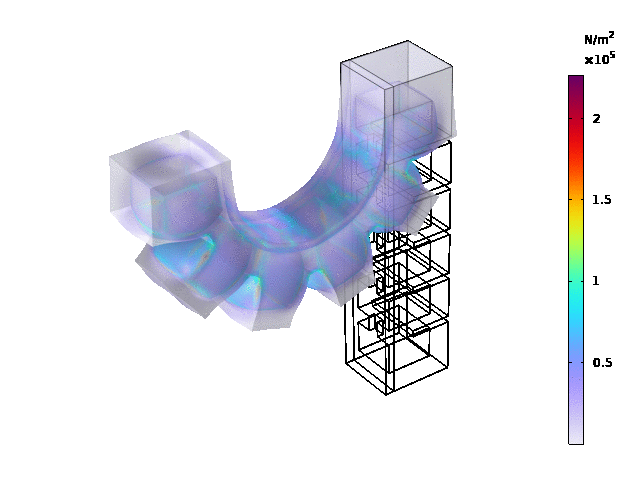
Reproduce the Simulation Results Using Another 3D Model

The following model was designed using information provided by Soft Robotic Gripper from www.instructables.com with SolidWorks 2023.

我用夸克网盘给你分享了「Soft Robotic Gripper.SLDPRT」，点击链接或复制整段内容，打开「夸克APP」即可获取。 /052439QiRT:/ 链接：https://pan.quark.cn/s/72cf82e697bb

我用夸克网盘给你分享了「Reproduce Using Another 3D Model.mph」，点击链接或复制整段内容，打开「夸克APP」即可获取。 /107e39RNsz:/ 链接：https://pan.quark.cn/s/296741996da9

The load type is pressure $p = \mathrm{pressure} \times \mathrm{ramp}$ , and ramp was set to range(0.01,0.01,0.3), pressure was set as 25[kPa].

Footnotes

1. M. S. Xavier, A. J. Fleming, and Y. K. Yong, “Finite Element Modeling of Soft Fluidic Actuators: Overview and Recent Developments,” Advanced Intelligent Systems, vol. 3, no. 2, p. 2000187, Feb. 2021, doi: 10.1002/aisy.202000187. ⤴

2. W. M. Lai, D. Rubin, and E. Krempl, Introduction to continuum mechanics, 4th ed. Amsterdam Boston: Butterworth-Heinemann/Elsevier, 2010. Page 111. ⤴

3. A. Ali, M. Hosseini, and B. B. Sahari, “A Review of Constitutive Models for Rubber-Like Materials,” AJEAS, vol. 3, no. 1, pp. 232–239, Mar. 2010, doi: 10.3844/ajeassp.2010.232.239. ⤴

4. D. Steck, J. Qu, S. B. Kordmahale, D. Tscharnuter, A. Muliana, and J. Kameoka, “Mechanical responses of Ecoflex silicone rubber: Compressible and incompressible behaviors,” Journal of Applied Polymer Science, vol. 136, no. 5, p. 47025, 2019, doi: 10.1002/app.47025. ⤴